量子优化打破质疑
FUTURE远见| 2021-11-08
Future|远见
Future|远见future选编
近期,IBM、亚马逊等互联网巨头相继推出量子信息新进展,各国大力支持。上海也发布一份重要文件,着重强调了「前瞻布局量子信息」。量子产业势头正猛,也有一些人质疑,会不会是炒作?量子计算目前的应用方向主要在优化、模拟等方面。今天就量子优化打破质疑。
优化问题无处不在,我们花费大量时间凭直觉去解决它们。当我们试图找出上下班的最短路线时,当我们寻找一家餐厅既好吃又健康时,当我们试图预测超市的哪个收银台移动速度最快时,我们都会遇到优化问题。对于更复杂的优化问题,我们使用经典计算机运行算法来寻找可能的最佳解决方案,但这些问题很快变得异常困难且计算成本高昂。长期以来,研究人员一直认为量子计算机可以更快、更准确地解决这些问题。

01 什么是量子优化
多年以来,这些理论上的提高使得量子科学家们非常兴奋。部分原因是优化问题无处不在。量化专家可以使用它们来代表财务规划、供应链管理、土木工程和无数其他领域中的大量重要且极具价值的现实世界问题。过去,人们倾向于相信量子优化的突破可以改变世界,比如缩短数百万英里的供应链,应对气候变化,甚至消除交通拥堵。然而,越来越多的专家表示,这些的说法太夸张了,尤其是在涉及现有的量子优化算法时,算法需要被进一步的研究来释放该领域的潜力。
与经典算法相比,我们今天拥有的量子算法只提供适度的加速。当涉及到特别大的优化问题和其他特定情况时,这些适度的改进可能很重要,但在许多其他情况下,你几乎不会注意到差异。
另一方面,如果研究人员可以找到某一个优化问题,量子计算机可以为其提供指数级别的加速,这种进步可能会永远改变这个领域和世界。一般来说,这些具有指数级加速的问题才是量子计算机真正会被应用的地方。量子计算机似乎没有为黑盒优化问题提供指数加速。黑盒优化是指我们对试图从中找到最佳解决方案的数据集一无所知。但是,在你对数据了解得更多的情况下,可能会有一些指数加速。这就是为什么量子优化算法依旧值得被重视。
但是要理解为什么量子优化是这种情况,我们首先需要了解什么是优化问题,经典计算机如何处理它们,以及量子计算机如何改进经典优化技术。
02 优化是寻求可能最好的解决方案
优化问题的目标是,找到可能最好的解决方案,方法是在满足某些限制条件的情况下改变某些变量的值。即,从有限(或可数无限)可能的解决方案集中找到最好的或「最佳」解决方案。例如,我们可以将流行的益智游戏数独视为一个优化问题,它要求玩家用数字填充 9x9 网格,使得每行、每列和 3x3 子网格都包含 1-9 的所有数字。在未解决的数独谜题中,每个空单元格代表玩家必须计算以解决问题的「决策变量」,而游戏规则本身代表玩家必须满足以实现最佳解决方案的约束。
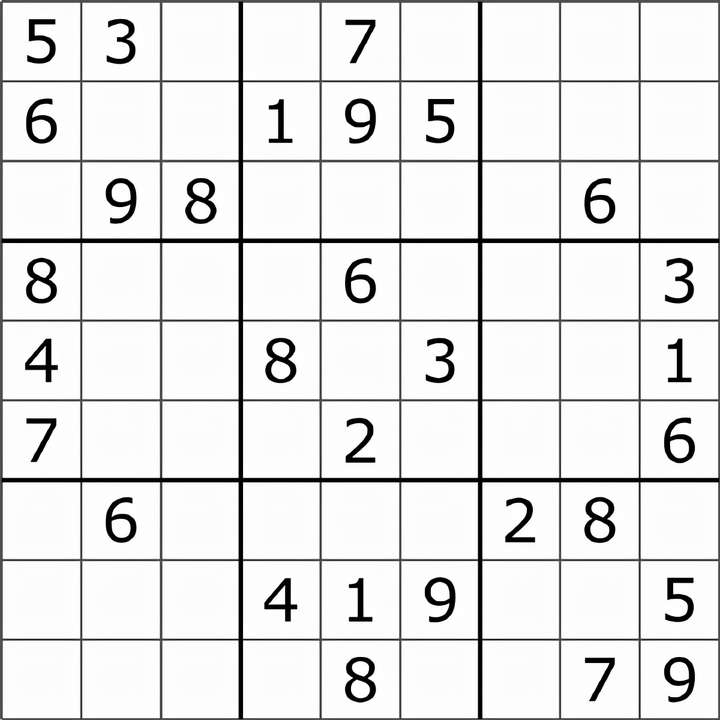

计算机如何解决这样的问题?嗯,有许多不同的优化算法以不同的方式对问题进行建模。
「你看一个简单的梯度下降算法,」 IBM 研究员和优化专家 Srinivasan Arunachalam 说。「梯度下降是用于优化的最基本算法,」他说,它也恰好是机器学习的主力——但那是另一个故事。
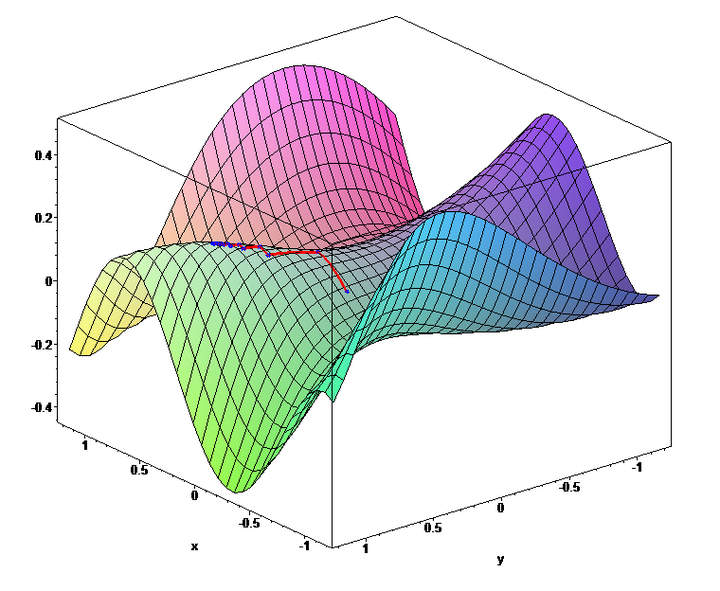
在数学中,梯度只是对特定线或表面的方向和陡度的描述。你几乎可以将任何优化问题表示为数学函数,也可以将任何数学函数以图形方式表示为线或多维曲面,具体取决于函数包含的变量数量。具有一个变量的函数描述一条线,具有两个变量的函数描述平面的形状,等等。想想那些凸起的地形地球仪,你可能会在学校教室里看到那种带有凹凸不平的地形,让你用手指感受喜马拉雅山的高度和大平面的平坦度。这些只是 3 维高度图,一个函数,其中两个变量是纬度和经度,函数的输出是海拔。
以这种方式描述优化问题通常会给你一些看起来像某个山区的地形图,充满了丘陵和山谷。在优化问题,在那些山谷最低点通常代表了最优化的解决方案,而山上的峰值表示最不优化的解决方案。这就是为什么它被称为「梯度下降」。你的最终目标是一路走到地图的最低点。然而,这可能会变得具有挑战性,因为通常无法鸟瞰整个函数。事实上,你看不到周围环境之外的任何东西。就好像你在晚上下山,在黑暗茂密的森林中挑选自己的路。
03 经典优化的困境
在经典计算中,到达地图上最低点的唯一方法(最优解)是首先查看你周围的环境,然后找出局部梯度哪个方向上升,哪个方向下降,然后朝着似乎正在走下坡路的方向迈出了一步。「标准的梯度下降从某个点开始,计算该点函数的梯度,然后……它决定我应该走到哪里,」Arunachalam 说,该决定由「梯度更新规则」控制,该规则确定算法如何随着每次新计算而移动。
在梯度下降中,你采取的每一步都需要进行全新一轮的计算,而且你永远无法 100% 确定你正在走向整个地图的最低点。你可能只是前往远离真正最低点(即「全局最低点」)的某个浅谷。这就是梯度下降对于经典计算机而言如此具有挑战性且计算成本高的部分原因。每个单独步骤背后的计算本身都相当耗费资源。同时,复杂的优化问题可能需要数百万步才能收敛到全局最小值。
这是大量的计算。让我们来看看量子计算机如何使这个过程更加高效。
04 高效的量子优化
几十年来,量子研究人员一直相信量子计算机可能为上述经典方法提供适度的改进。这并不是因为研究人员认为量子计算机可以完全取代经典计算机,无条件地比经典计算机更快地执行梯度下降算法。相反,这是因为量子计算机可以更快地执行算法过程中的几个特定步骤。
根据 IBM 的 GiacomoNannicini 的说法,同样的推理适用于大多数理论上的量子优势案例。「我会说,我们认为优化问题具有量子优势的原因与我们能够在其他领域找到优势的原因完全相同,」他说。由于量子计算机应该能够在优化算法所需的某些任务上胜过经典计算机,因此它们可以作为子程序集成到更广泛的算法中。

为了更清楚地解释这一点,我们将进行一些数学运算。别担心,我们会保持简单阐述。如果你不熟悉线性代数,你只需要知道「向量」只是一个数字列表。该列表中的每个项目或元素代表优化问题中的一个变量。
假设你的优化问题可以表示为一个线性函数f,这意味着描述它的函数只是两个向量的内积——一个向量乘以另一个得到一个数字。其中一个向量是固定的,但未知。我们将其称为向量a (即 [a₁, a₂, a₃...aₙ])。另一个是你的输入向量x (即 [x₁ , x₂ , x₃...xₙ])。如果向量都有n个元素,那么取内积只是意味着将相应的元素相乘并将它们相加,如下所示:[(a₁*x₁) + (a₂*x₂) + (a₃*x₃) + ... (aₙ*xₙ)]。
梯度下降算法中的基本程序之一是计算某个给定点x的函数f的梯度。当你决定梯度下降的下一步时,这是必不可少的信息。如果f (x₁, x₂…xₙ) = (a₁* x₁ ) + (a₂*x₂) + ... (aₙ*xₙ),那么你在给定点x寻找的梯度是一个未知向量a。你的工作是计算它。
例如,如果你的向量每个只有三个元素,你首先将x设置为 【1 , 0, 0]。当你将其乘以未知向量a 时,你会得到 [( a₁*1) + (a₂*0) + (a₃*0)]。这仅仅是a₁。然后,你可以对向量a 中的每个其他元素执行相同的操作,将输入向量x设置为 [0, 1 , 0] 以确定a₂的值,然后将其设置为[0, 0,1 ] 来确定a₃的值。

这看起来很容易,但是当你处理的矢量具有上百个元素时,事情变得棘手了。在像这样的经典机制中,你必须对每个单独的元素进行查询,以找出向量a的内容。最终,这不是很有效。研究人员认为,与经典计算机相比,量子计算机可以为此类任务提供多项式加速(特别是二次项加速)。
「量子上,有一个很好的算法叫做 Bernstein-Vazarani,」 Arunachalam 说。这种著名的算法允许你仅使用一个查询来确定向量a,而不是传统方法所需的 n 个查询。那是因为 Bernstein-Vazarani 以量子方式执行查询——查询是由 x 的所有元素叠加而成的。从那里,你应用量子傅里叶变换( QFT ),就像那样,傅里叶变换会为你呈现向量a。
「你基本上可以通过对 x 进行一次量子查询来了解向量 a 的全部,但在经典计算机上通常你需要 n 次查询,」Arunachalam 说,这实质上是表明量子计算机应该能够为梯度下降提供二次加速的基本思想。但是,重要的是要注意,这是一个简化的示例,因此在总体方案中,这种加速仍然被认为相对较小。
「这个例子只是一个基本的线性函数,今天的经典计算机可以轻松处理,」Arunachalam 说。「当你将这些相同的原理应用于多维非线性函数时,真正的量子优势就会出现,这在现实世界的优化问题中更为常见,而对于经典计算机来说则困难得多。」在 2017 年的一篇论文中,Arunachalam 和他的合著者率先展示了使用多维函数的量子梯度计算实现二次加速。

一旦你理解了这个逻辑,就可以很容易地扩展它来为各种凸优化技术提供量子改进,其中梯度下降只是一个例子。凸优化是一个广泛的类别,包括梯度下降和许多其他优化方法。它在为我们今天拥有的大多数自动化技术提供动力的经典机器学习系统中发挥着巨大的作用。还可以应用凸优化技术获得更专业的二次加速,量化专业人士将其用于各种行业应用。
二次加速,以及一般的多项式加速,可能不如量子研究的其他一些领域中发现的指数加速那么大,但它们仍然很重要。在优化问题的背景下尤其如此,在这种情况下,每一个微小的改进都可以带来巨大的现实世界价值。然而,对于许多量子研究人员来说,多项式加速还不足以使它们成为首要研究重点。
05 指数级差异
当我们谈论量子优势,特别是「量子加速」时,我们实际上是在谈论与经典计算机相比,量子计算机如何在某些算法任务上表现出改进的时间复杂度。时间复杂度是一种描述运行算法需要多少时间(或多少计算步骤)的方式,而且至关重要的是,它还描述了随着输入的大小的改变,运行时间如何变化。
在多项式加速中,「多项式」一词仅指描述两种不同时间复杂度之间关系的数学函数类型。例如,如果经典计算机需要 N² 步来完成 n 个输入的任务,而量子计算机只需要 N 步来完成 n 个输入的任务——这就是二次加速。令人印象深刻,对吧?量子计算机可以在 10 步中完成一些经典计算机需要 100 步才能完成的事情。这听起来是一个相当大的改进。

但事实是,像这样的加速在宏观计划中相对微不足道,尤其是在短期内。一个指数加速会更加显著。例如,如果一台经典计算机需要 2ᴺ 来完成 n 个输入的任务,而一台量子计算机只需要 N 步来完成同样的事情,那就是巨大的差异。这意味着量子计算机可以在 10 步中完成一些事情,而经典计算机需要 1024 步,并且随着输入的大小变大,差异会急剧增加。
Arunachalam 还指出,经典计算领域在硬件开发方面已经相当成熟,而量子硬件开发才刚刚起步,还有巨大的发展空间。
对于 IBM 的 GiacomoNannicini 来说,考虑到数学优化的巨大经济和社会价值,一旦量子硬件成熟,即使在解决优化问题方面的适度加速也值得付出努力,这一点很重要。「一般来说,在工程和商业的很多领域,我们经常解决优化问题,」他说。「优化是如此有用,而且它在行业中的使用如此普遍,如果你能够获得任何优势,它将使你的业务受益。」
作者:Robert Davis,IBM Quantum 和 Qiskit 技术作家
数独图源:
https://commons.wikimedia.org/w/index.php?curid=57831971
原文链接:
https://medium.com/qiskit/cutting-through-the-hype-of-quantum-optimization-6d4b5c95e377
Warning: Invalid argument supplied for foreach() in /www/wwwroot/www.futureyuanjian.com/wp-content/themes/future/single-news.php on line 41



